반응형
제곱
같은 수를 두번 곱한 것.
*마이너스 일 때
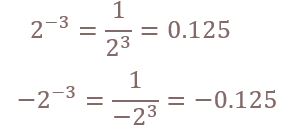
System.out.println(Math.pow(2,3));
//결과 8.0
System.out.println(Math.pow(2,-3));
//결과 0.125 제곱이 -일 경우 분모로 들어감.
System.out.println(Math.pow(-2,-3));
//결과 -0.125
//pow 만들기
static double pow(int a, double b){
double result = 1;
boolean isMinus = false; //음수인지 판별.
if (b == 0) {
return 1;
} else if(b < 0) { //b가 음수인 경우
b *= -1;
isMinus = true;
}
for (int i = 0; i < b; i++) {
result *= a;
}
return isMinus ? 1 / result : result;
}
*거듭제곱 - 같은 수를 거듭해 곱함. (ex) 2^3 = 2x2x2)
제곱근 (=root, √)
a를 제곱하여 b가 될 때 a를 b의 제곱근이라 한다.
ex) √4 = √2^2 = 2
a^x ==> a : 밑 x : 지수
System.out.println(Math.sqrt(16));
//결과 4.0
//pow로 구하기
System.out.println(Math.pow(16, 1.0/4));
//결과 2.0 16의 지수가 4분의 1이 됨.
//sqrt 구하기
static double sqrt(int a){
double result = 1;
//바빌로니아 방법. 많이 할수록 더 가까운 근삿값 구하기 가능. a= N
for (int i = 0; i < 10; i++) {
result = (result + (a/ result)) /2;
}
return result;
}
로그(log)
log_ab = a가 b가 되기 위해 제곱해야하는 수

System.out.println(Math.E); //자연 상수
System.out.println(Math.log(2.718281828459045)); //log의 밑수가 자연상수 결과 : 1.0
System.out.println(Math.log10(1000)); //log의 밑수가 10 결과 : 3.0
System.out.println(Math.log(4) / Math.log(2)); //다른 밑수 구하기 결과 2.0
* 참고용) 절대 값
System.out.println(Math.abs(5));
System.out.println(Math.abs(-5));
반응형
'기초수학' 카테고리의 다른 글
| 시간복잡도(Time complexity)와 공간복잡도(Space complexity) (0) | 2024.02.27 |
|---|---|
| 점화식(Recurrence), 재귀함수 (0) | 2024.02.27 |
| 조합 (Combination) (0) | 2024.02.27 |
| 순열(Permutation), 팩토리얼(Factorial) (0) | 2024.02.27 |
| 경우의 수 (합의 법칙, 곱의 법칙) (0) | 2024.02.26 |
