반응형
점화식
어떤 수열의 일반항을 그 이전의 항들을 이용해 정의한 식
ex) 피보나치 수열
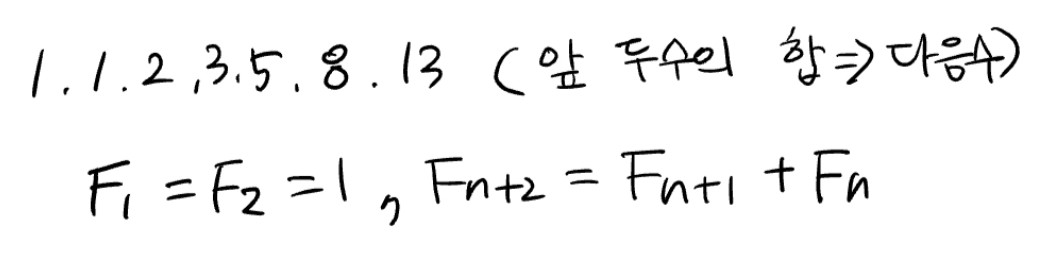
재귀함수
어떤 함수가 자신을 다시 호출해서 작업을 수행하는 방식
반환타입 함수이름 (매개변수) {
종료조건 (없을 시에는 무한루프됨.)
...
함수이름(...)
}
3씩 곱해질 때의 n번째 수 구하기
// 1, 3, 9, 27, ... 의 n번째 수
int n = 4;
int result = 1;
for (int i = 0; i < n; i++) {
if (i == 0) {
result = 1;
} else {
result *= 3;
}
}
System.out.println(result);
//재귀함수로 구현
static int recursion(int n) {
if(n == 1) {
return 1;
}
return 3 * recursion(n-1);
} //결과 : 27

위의 재귀함수로 구현한 것을 그림으로 그리면 이렇게 된다.
피보나치 수열 n번째 수 구하기
// 1, 1, 2, 3, 5, 8, 13, ...의 n번 째 수
n = 6;
result = 0;
int a1 = 1;
int a2 = 1;
if(n < 3) {
result = 1; //3보다 적을 때는 1,1이니까
} else {
for (int i = 2; i < n; i++) { //2부터 시작
result = a1 + a2;
a1 = a2; //최신 수로 변경
a2 = result;
}
}
System.out.println(result);
//재귀함수로 구현
static int recursion3(int n) {
if(n < 3){
return 1;
}
return recursion3(n-2) + recursion3(n-1);
//결과 8
재귀함수를 설명하면 이렇게 된다.
팩토리얼 구현
static int factorial(int n) {
if (n == 1) {
return 1;
}
return n * factorial(n - 1);
}최대공약수 구현
static int gcd(int a, int b) {
if (a % b == 0) {
return b;
}
return gcd(b, a % b);
}예를 들어보면,

이렇게 진행된다.
반응형
'기초수학' 카테고리의 다른 글
| 시간복잡도(Time complexity)와 공간복잡도(Space complexity) (0) | 2024.02.27 |
|---|---|
| 제곱과 로그 (0) | 2024.02.27 |
| 조합 (Combination) (0) | 2024.02.27 |
| 순열(Permutation), 팩토리얼(Factorial) (0) | 2024.02.27 |
| 경우의 수 (합의 법칙, 곱의 법칙) (0) | 2024.02.26 |
